Tuesday April 30, 2024

Udemy courses in university mathematics

In August 2020 I published my first course on Udemy. In May 2021 I decided to quit my job at the university and start recording my own courses full time. I plan to record a large part of a typical curriculum in undergraduate mathematics. You will find here the information about all my courses:

PhD thesis and examination

On September 25, 2009, I presented my thesis and defended it, with success. You can find the details, including the full thesis as published, a video of my presentation, the slides, and photos, on a separate page.
I did my Ph.D. studies in Uppsala, in the Department of Mathematics of Uppsala University. Together with my advisor Professor Christer Kiselman and my colleague Shiva Samieinia we formed a research group in Digital Geometry. I defended my thesis on 25 September 2009. My research was focused on arithmetic properties of digital lines in two dimensions. I was mainly interested in the lines with irrational slopes, which leads to research on Sturmian words. I formulated a new description of upper mechanical words with irrational slopes. The description was based on continued fractions. I also formulated a new fixed-point theorem for Sturmian words, which I presented on the conference Words 2009. During my Ph.D. studies I felt inspired by the work of Valérie Berthé, Damien Jamet and Thomas Fernique.

For more details about my research, see the list of my publications and my CV. The current page describes only my research done before 25 September 2009. From October 2009 till July 2010 I studied applications of discrete mathematics (various combinatorial tools, Petri nets, traces) in computer science. Since August the 1st, 2010 I have been working on a new medical journal iotaMed.

Sturmian words with balanced construction - In Proceedings of Words 2009, the 7th International Conference on Words (Salerno, Italy), 14-18 September 2009. You can get a preprint here.

Abstract: In this paper we define Sturmian words with balanced construction. We formulate a fixed-point theorem for Sturmian words and analyze the set of all fixed points. The inspiration for this work came from the Kolakoski word and the general idea of self-reading sequences by Paun and Salomaa. The basis for this article is the author's earlier research on the influence of the continued fraction elements in the expansion of a positive irrational a less than 1 on the construction of runs for the upper mechanical word with slope a and intercept 0.

Continued Fractions, Fibonacci Numbers, and Some Classes of Irrational Numbers - published in Acta Mathematica Academiae Paedagogicae Nyiregyhaziensis vol. 26(1), 2010.

Abstract: In this paper we define an equivalence relation on the set of positive irrational numbers less than 1. The relation is defined by means of continued fractions. Equivalence classes under this relation are determined by the places of some elements equal to 1 (called essential 1's) in the continued fraction expansion of numbers. Analysis of suprema of all the equivalence classes leads to a solution which involves Fibonacci numbers and constitutes the main result of this paper. The problem has its origin in the author's research on the construction of digital lines and upper and lower mechanical and characteristic words according to the hierarchy of runs.

Two Equivalence Relations on Digital Lines with Irrational Slopes. A Continued Fraction Approach to Upper Mechanical Words - Theoretical Computer Science 410 (2009) 3655-3669. You can get the paper here. If you don't have access to the journal you can email me for a reprint.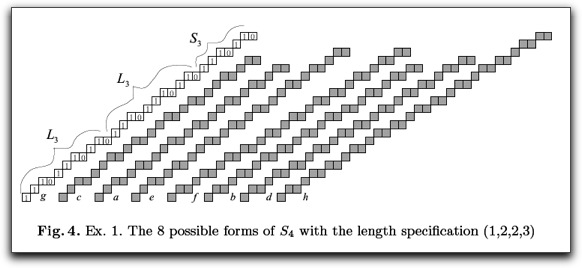

Abstract: We examine the influence of the elements of the continued fraction (CF) expansion of irrational positive a less than 1 on the construction of runs in the digitization of the positive half line y=ax or, equivalently, on the run-hierarchical structure of the upper mechanical word with slope a and intercept 0. Special attention is given to the CF elements equal to 1. We define two complementary equivalence relations on the set of slopes, based on their CF expansions. A new description of digital lines is presented; we show how to define a straight line or upper mechanical word by two sequences of positive integers, fulfilling some extra conditions. These equivalence relations and this new description enable us to analyze the construction of digital lines and upper mechanical words. The analysis of suprema of equivalence classes under one of these relations leads to a solution which involves Fibonacci numbers.

A Run-hierarchical Description of Upper Mechanical Words with Irrational Slopes Using Continued Fractions - A reviewed conference paper. Published in the Proceedings of the 12th Mons Theoretical Computer Science Days JM 2008 (27-30 August 2008, Mons, Belgium). You can get a preprint here

Abstract: The main result is a run-hierarchical description (by continued fractions) of upper mechanical words with irrational positive slopes less than 1 and intercept 0. We compare this description with two other methods of forming of such words. In order to be able to perform the comparison, we present a quantitative analysis of our method. We use the denominators of the convergents of the continued fraction expansion of the slope to compute the length of the prefixes obtained by our method. Due to the special treatment which is given to the elements equal to 1, our method is, in some cases, more efficient than the two other methods. This new method reflects the hierarchy of runs, by analogy to digital lines.

Run-hierarchical structure of digital lines with irrational slopes in terms of continued fraction and the Gauss map. Published in DGCI 2008 Special Issue in Pattern Recognition. Publication reference: Pattern Recognition 42 (2009) 2247-2254. You can get the paper here. If you don't have access to the journal you can email me for a reprint.

Abstract: This paper is an extended version of the paper to DGCI 2008.

Continued Fractions and Digital Lines with Irrational Slopes - A peer reviewed conference paper. Published in the Proceedings of the 14th International Conference on Discrete Geometry for Computer Imagery (16-18 April 2008, Lyon, France). Publication reference: LNCS 4992, pp. 93-104, 2008. You can get the paper here. If you don't have access to the journal you can email me for a reprint.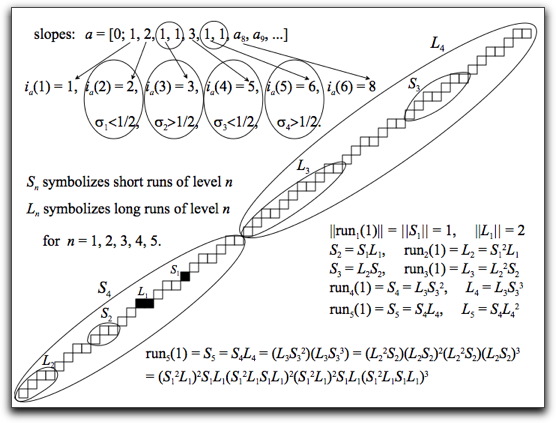

Abstract: This paper expands on previous work on relationships between digital lines and continued fractions (CF). The main result is a parsimonious description of the construction of the digital line based only on the elements of the CF representing its slope and containing only simple integer computations. The description reflects the hierarchy of digitization runs, which raises the possibility of dividing digital lines into equivalence classes depending on the CF expansions of their slopes. Our work is confined to irrational slopes since, to our knowledge, there exists no such description for these, in contrast to rational slopes which have been extensively examined. The description is exact and does not use approximations by rationals. Examples of lines with irrational slopes and with very simple digitization patterns are presented. These include both slopes with periodic and non-periodic CF expansions, i.e. both quadratic surds and other irrationals.

Digital Lines with Irrational Slopes - An article I wrote on the generalization of digital lines for irrational slopes. In February 2007 it was accepted for publication in the Theoretical Computer Science (Elsevier). Publication details: Theoretical Computer Science 377 (2007) 157-169. You can get the paper here. If you don't have access to the journal you can email me for a reprint.


If this excerpt doesn't turn you on, I don't know what will.

Digital Lines - a presentation

All this is stuff I made as part of the PhD program at Uppsala University.

Digital Lines - a presentation I gave internally at the University December 15, 2003. This link will run the presentation within your browser. 

You can also retrieve it as a powerpoint file.

Note: if you want to download the presentation to your own computer, right-click the link above and choose "Save Target As..." or whatever is the equivalent command on your machine.

And, I can't help telling you about this, but I've been interviewed for the Swedish radio! Yes! Or TV, maybe, I don't know. And they put me on their web-site! I'm very happy! I think!

January 2005, I gave another presentation on Digital Lines, this time concentrating on theorems and proofs instead of algorithms. You can view it as a presentation online or get it as a pdf file (with the notes included in both cases).

 

Complex numbers - a Mathematica notebook by me (Hania). It's in Dutch, since it was written for Dutch-speaking students at the University of Brussels.

Do either one of the following (we recommend the first alternative - or, if you prefer, the first "choice" in the set of "alternatives" - euh... just joking, you know what... pick the first and I'll shut up):

  • Get "Complex numbers" as Mathematica notebook:

    • First, download and install the free Mathematica reader from Wolfram: click here.

    • Then, download my notebook file and view it: click here.

     

  • Get "Complex numbers" as PDF file:
    • First, download the free Acrobat reader from Adobe: click here.
    • Then, download my PDF file and view it: click here.

     

  • If you already have the full commercial version of Mathematica (3.0 or later), you're much better off downloading the version of the notebook "without output", as it's much smaller, then opening it in Mathematica and evaluate the whole notebook through the "Kernel" menu.
    • To download the notebook "without output", click here.

     

  • The University of Brussels has the same notebook in an online, slightly interactive, version: click here for the link

Complex polynomials - the sequel to the above notebook. In its complete form, including evaluation outputs, this one is really large. It's just as flabbergastingly large (27 Mb uncompressed, 7.5 Mb compressed) in the evaluated form as it is small and nifty (200k) in its non-evaluated form. So if you have the full version of Mathematica (3.0 or later), take the small one. If you only have the free Mathematica reader, you have to download the humonguous one. It's compressed into a selfextracting form for IBM PC compatibles. If you can't use that, drop me a line and we'll figure something out.

  • Get "Complex polynomials" as Mathematica notebook:
    • First, download and install the free Mathematica reader from Wolfram: click here.
    • Then, download my notebook file: click here.

     

  • If you already have the full commercial version of Mathematica (3.0 or later), you're much better off downloading the version of the notebook "without output", as it's much smaller, then opening it in Mathematica and evaluate the whole notebook through the "Kernel" menu.
    • To download the notebook "without output", click here.

     

  • The University of Brussels has this one too online: click here for the link.

Complex numbers and geometry - the third in the series. Shows how to use complex numbers to simplify solving problems in geometry.

  • Get "Complex numbers and geometry" as Mathematica notebook:
    • First, download and install the free Mathematica reader from Wolfram: click here.
    • Then, download my notebook file as a self-extracting exe file: click here.

     

  • If you already have the full commercial version of Mathematica (3.0 or later), you're much better off downloading the version of the notebook "without output", as it's much smaller, then opening it in Mathematica and evaluate the whole notebook through the "Kernel" menu.
    • To download the notebook "without output", click here.

     

TOP